 |
|
 |
 |
|
 |
OBJECTIVE
|
|
|||||||||||||||
TOPICAL LINKS
|
|
|||||||||||||||
COMPARISON DATA SET
|
Set up a test data set similar to Table 6.7 but for GNSS constellations? | |||||||||||||||
IMPLEMENTATION ISSUES
|
||||||||||||||||
RESPONSE
|
I think you misinterpret equation (6.15). I don’t know who introduced it, but it provides apparently some confusion into the chapter 6.3. It is a general equation which indicates that the tides coefficients are time dependent. These ΔCnm/ΔSnm (function of the argument ϑ) are not given in any file. The so called DelC/DelS coefficients (from the file) are well described in equation (6.21) and do not rely on equation (6.15). Now, by definition of the harmonic coefficients, the zonal terms of retrograde waves are identical to the zonal terms of prograde waves, for there is no more dependence in longitude (m=0); that is why the (n,0) coefficients of prograde waves are doubled and those ones of retrograde waves are put to zero. Maybe you could contact Richard Ray (GSFC) for more explanations if needed. He could provide you the GOT4.7 models as well. | |||||||||||||||
RESPONSE
|
I am still confused about how to interpret the files given in the ftp area in the standards for fes2004, and how to relate the equations to the files and to your notation given the earlier email. (By the way is there a reference to where these files came from and/or who generated them?) Lets start with the fes2004_Cnm-Snm.dat where the column headings seem to match the symbols being used in the standards. The coefficients in this file appear as if they should be directly used in Equation 6.15 to generate time dependent Cnm and Snm coefficients when the cos(ϑ+) and sin(ϑ+) are evaluated. So according to the equation (6.15) one should have an equivalence such as: ΔC+ = C+cosϑ+ + S+sinϑ+ for prograde waves and ΔC- = C-cosϑ- + S-sinϑ- for retrograde waves ΔS+ = -C+sinϑ+ + S+cosϑ+ ΔS- = C-sinϑ- – S-cosϑ- I interpret your equations to translate as: C+ = DelC+ ; S+ = DelS+; C- = DelC- ; S- = DelS- from the table headings and ΔC+ is ΔCnm+ and ΔS+ is ΔSnm+ and similarly for the minus sign values. I’m also assuming that at any time (i.e., independent of the value of ϑ+ or ϑ- (you never define what these angles are) that the zonal ΔSn0 coefficients should be zero i.e., 6.15 should generate a set of spherical harmonic coefficients that can be used to compute the potential at any latitude and longitude in the standard way). Below are the coefficients for degree 2 and 3 M2 zonal terms and if I use your formulas above the ΔS+ will be non-zero because DelC+ and DelS+ are non-zero and the DelC- and DelS- terms are zero so there is no way for the retrograde wave to cancel the prograde wave for the ΔS zonal terms. For me the question is: What formulation generates non-zero Sn0 coefficients when we are generating a standard spherical harmonic expansion? If we interpret the table to be Cnm and Snm directly (i.e. DelC+ = Cnm cos, DelS+ = Cnm sin, DelC- = Snm cos and DelS- Snm sin, then the zonals look perfectly reasonable but this is not what the standards say these coefficients are. A citation to where and from whom these tables came would useful.
|
|||||||||||||||
RESPONSE
|
It seems to me that the equation (6.15) is confusing when associated with the FES 2004 files.
The file: fes2004.dat gives the original spherical harmonic coefficients as expressed in the chapter 6.3.1 of the Conventions. This file gives the tidal water height (in cm) according to the classical surface potential expansion. Example for FES 2004: Ocean tide model: FES2004 normalized model (fev. 2004) up to (100,100) in cm (long period from FES2002 up to (50,50) + equilibrium Om1/Om2, atmospheric tide NOT included)
The equation 6.15 gives the transformation into Stokes’ coefficients and relies on the other file given as: fes2004 Cnm-Snm.dat Your example: % head fes2004 Cnm-Snm.dat Coefficients to compute variations in normalized Stokes coefficients (unit = 10^-12) Ocean tide model: FES2004 normalized model (fev. 2004) up to (100,100) (long period from FES2002 up to (50,50) + equilibrium Om1/Om2, atmospheric tide NOT included)
So according to the equation (6.15) one should have an equivalence such as: ΔC+ = C+cosϑ+ + S+sinϑ+ for prograde waves and ΔC- = C-cosϑ- + S-sinϑ- for retrograde waves ΔS+ = -C+sinϑ+ + S+cosϑ+ ΔS- = C-sinϑ- – S-cosϑ- where ϑ+/- is the argument of the wave. The ΔC/S coefficients are hence time depending. But the DelC/S coefficients you mentioned are described in equation (6.21). And take care that the phase convention given in table (6.6) is then applied. That means for instance that you have to apply a phase difference of pi for Om1. |
|||||||||||||||
POTENTIAL
|
The formulation in the conventions equation 6.1 (Page 89) is a prograde-retro grade representation as shown below:
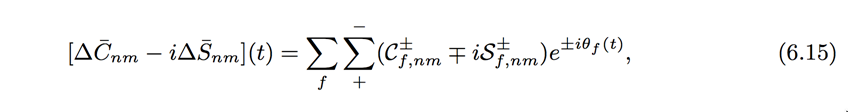
From the conventions page 91 it says: "For direct use in Equation (6.15), the coefficients C± and S± for the main tidal waves C+-f,nm S+-f,nm of FES2004 can be found at: fes2004 Cnm-Snm.dat " But the file pointed to at the ftp site, looks to us to be C_nm Cos/C_nm Sin Snm Cos/S_nm Sin formational because for all the zonal terms, the columns labeled DelC- DelS- are zero Whereas in the prograde/retro formulations, the zonal terms have equal DelC+ and DelC- terms which sum to give C_nm and difference to given S_nm (and hence when they are equal for zonals, the Sn0 terms are zero). head fes2004 Cnm-Snm.dat Coefficients to compute variations in normalized Stokes coefficients (unit = 10^-12) Ocean tide model: FES2004 normalized model (fev. 2004) up to (100,100) (long period from FES2002 up to (50,50) + equilibrium Om1/Om2, atmospheric tide NOT included)
We are curious what other ACs have done and whether we have completely misinterpreted the equations and table? - Tom Herring. |
| Send comments to IGS ACC | Privacy Policy | 3rd January 2018 |